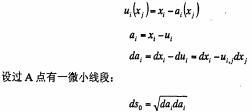第3章 致密成型過(guò)程有限元非線性分析
3.1有限元ANSYS軟件介紹
ANSYS軟件是融結(jié)構(gòu)、流體、電磁場(chǎng)、聲場(chǎng)、和耦合場(chǎng)分析于一體的大型通用有限元分析軟件。由世界最大的有限元分析軟件公司之一的美國(guó)ANSYS開發(fā),它能與多數(shù)CAD軟件界面,實(shí)現(xiàn)數(shù)據(jù)的共享和交換,如PRO/E、UG、I-DEAS、CADDS及AutoCAD等,是現(xiàn)代產(chǎn)品設(shè)計(jì)中的高級(jí)CAD工具之一。
ANSYS是一種應(yīng)用廣泛的商業(yè)套裝工程分析軟件。所謂工程分析軟件,就是根據(jù)機(jī)械系統(tǒng)受載時(shí)的應(yīng)力、應(yīng)變、溫度、位移等變化,得知機(jī)械結(jié)構(gòu)系統(tǒng)負(fù)載后的狀態(tài),判斷是否滿足設(shè)計(jì)要求。由于機(jī)械結(jié)構(gòu)負(fù)載較多,而且?guī)缀谓Y(jié)構(gòu)也相當(dāng)復(fù)雜,普通的理論分析很難進(jìn)行,只有忽略一些條件,簡(jiǎn)化結(jié)構(gòu),采用數(shù)值模擬方法進(jìn)行分析。近年來(lái)由于計(jì)算機(jī)行業(yè)的快速發(fā)展,使得ANSYS等CAE軟件廣泛應(yīng)用在工程上,例如在機(jī)械、電子、機(jī)電、航空和土木等領(lǐng)域的使用,頗受各界好評(píng)。
使用有限元軟件,能夠降低成本,縮短設(shè)計(jì)時(shí)間。2000年11月北京飛箭軟件公司和中國(guó)科學(xué)院聯(lián)合成功研發(fā)了世界上第一個(gè)可通過(guò)互聯(lián)網(wǎng)使用的有限元分析軟件,大家可以通過(guò)網(wǎng)絡(luò)平臺(tái)共享資源,使我國(guó)在研究有限元法及應(yīng)用方面獲得了突破性進(jìn)展,該套系統(tǒng)突破了國(guó)內(nèi)外的通用有限元軟件只適用于特定領(lǐng)域和特定有限元問題的限制,使廣大科學(xué)家和工程師從重復(fù)、繁瑣的編程工作中徹底解放出來(lái),原來(lái)人們需要數(shù)月才能完成的編程工作采用這一系統(tǒng)可以在數(shù)天甚至數(shù)小時(shí)內(nèi)完成。
ANSYS軟件有以下特點(diǎn):
1)前處理功能強(qiáng)。可以方便地構(gòu)造有限元模型、定義材料特性、邊界條件、各種荷載、建立約束方程;提供了強(qiáng)大的劃分網(wǎng)格工具,具有子結(jié)構(gòu)、子模型等高級(jí)功能。
2)分析能力強(qiáng)。包括結(jié)構(gòu)分析、電磁場(chǎng)分析、流體動(dòng)力學(xué)分析、聲場(chǎng)分析、電壓分析以及多物理場(chǎng)的耦合分析,具有多種方程求解器,求解精度高。
3)后處理功能強(qiáng)。可將計(jì)算結(jié)果以彩色等值線顯示,也可將結(jié)果以圖表、曲線形式顯示或輸出,可獲得任何節(jié)點(diǎn)、單元的數(shù)據(jù)。
4)開放型好。用戶可以在ANSYS系統(tǒng)上擴(kuò)展新的用戶功能。
3.2 有限元法基本理論
有限元法的基本思路可以歸結(jié)為,用較簡(jiǎn)單的問題代替復(fù)雜的問題然后再求解。它是將連續(xù)的求解域看成由許多稱為有限元的小的互連子域組成,對(duì)每個(gè)單元假定一個(gè)簡(jiǎn)單的近似解,將一個(gè)連續(xù)的問題簡(jiǎn)化為離散的有限個(gè)問題求解,然后推導(dǎo)求解域的滿足條件,來(lái)逼近或模擬原來(lái)的求解域。這個(gè)解不是準(zhǔn)確解,而是近似解。求解域被離散后,通過(guò)對(duì)其中各個(gè)子域進(jìn)行單元分析,再將所有子域按標(biāo)準(zhǔn)方法擬合,最終得到對(duì)整個(gè)物體的分析。
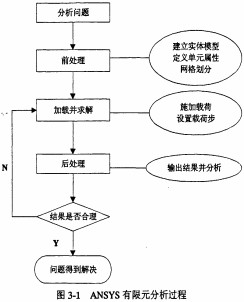
ANSYS有限元分析過(guò)程可概括如圖3-1
20世紀(jì)70年代,隨著計(jì)算機(jī)科學(xué)技術(shù)飛速發(fā)展,將計(jì)算機(jī)與有限元方法相結(jié)合,大大的減少了以前冗繁的計(jì)算,提高了計(jì)算速度。為工程計(jì)算以及數(shù)值模擬提供了一個(gè)寬廣的平臺(tái)。
對(duì)于材料的致密成型而言,有限元方法可以分為流動(dòng)型塑性有限元和固體型塑性成型有限元兩大類。流動(dòng)型塑性有限元包括剛粘塑性有限元和剛塑性有限元;固體型塑性成型有限元又包括彈粘塑性有限元和彈塑性有限元。流動(dòng)型塑性有限元不計(jì)材料的彈性變形,采用Levy-Mises方程作為本構(gòu)方程,固體型塑性成型有限元不但考慮彈性變形,還要考慮塑性變形,材料發(fā)生彈性變形時(shí)采用虎克定律,塑性變形區(qū)采用Prandtl-Reuss方程和Mises屈服準(zhǔn)則。
本文研究的生物質(zhì)秸稈是彈塑性材料,在施加壓力的條件下一開始生物質(zhì)秸稈會(huì)發(fā)生彈性變形,但是隨著擠壓的繼續(xù)進(jìn)行,它會(huì)發(fā)生較大的塑性變形,由于變形過(guò)程中接觸等條件不確定,流動(dòng)型塑性有限元方法不適合該變形過(guò)程。生物質(zhì)的材料屬性與金屬有很大的區(qū)別,固體型塑性成型有限元基本假設(shè)與生物質(zhì)秸稈有著很大差別,它主要是針對(duì)金屬材料建立起來(lái)的,例如金屬材料屬于單相介質(zhì),而生物質(zhì)秸稈是多相介質(zhì);生物質(zhì)秸稈成型機(jī)理要比普通金屬材料成型機(jī)理復(fù)雜很多,在靜壓屈服方面,生物質(zhì)秸稈不僅發(fā)生彈性體積變形,還會(huì)發(fā)生塑性體積變形,而金屬材料只發(fā)生彈性體積變形;在加載情況下,生物質(zhì)秸稈粒子會(huì)發(fā)生滑動(dòng)、滾動(dòng)、轉(zhuǎn)動(dòng)及壓碎等現(xiàn)象。
生物質(zhì)秸稈
顆粒燃料在致密成型時(shí),由于秸稈的材料特性問題,擠壓過(guò)程中變形比較明顯,屬于大變形問題,為幾何非線性問題。應(yīng)該采用有限元法大變形非線性進(jìn)行研究。生物質(zhì)秸稈致密成型的變化行為只有大變形彈塑性理論能夠比較準(zhǔn)確合理地描述,所以采用大變形彈塑性理論先對(duì)生物質(zhì)秸稈的壓縮變形進(jìn)行理論分析,然后建立方程,解決生物質(zhì)秸稈材料非線性問題。
幾何非線性問題主要分為兩類,一類問題為大位移大應(yīng)變,即大應(yīng)變引起大位移,其材料和幾何方程均為非線性:另一類問題為大位移小應(yīng)變,即在彈性極限范圍內(nèi),應(yīng)變很小,但是位移卻較大。生物質(zhì)秸稈致密成型屬于大位移大應(yīng)變問題,根據(jù)幾何非線性的條件,采用大變形理論來(lái)研究。
在生物質(zhì)秸稈的致密成型過(guò)程中,由于物料具有可壓縮性,物料之間相互擠壓空隙減少且逐漸發(fā)生變形,秸稈形狀有很大改變,受屈服的影響,變形和致密過(guò)程共存,材料壓縮過(guò)程中存在接觸非線性、材料幾何大變形和塑性變形,且需要考慮靜水壓力的影響,問題分析起來(lái)比較復(fù)雜,想要求得精確解比較困難。有限元的觀點(diǎn)則為單元發(fā)生很大變形且單元之間有很大的位移,成為研究生物質(zhì)秸稈致密成型的一種有效手段。
秸稈、木屑等生物質(zhì)材料屬于非連續(xù)介質(zhì),不能用普通的連續(xù)介質(zhì)力學(xué)進(jìn)行研究,但是由于目前非連續(xù)介質(zhì)力學(xué)的基本理論研究還不夠完善,在研究秸稈等生物質(zhì)致密成型中物料的擠壓變形時(shí),使應(yīng)用受到一定限制。為了方便研究問題,將秸稈、木屑等生物質(zhì)看作“可壓縮的連續(xù)體”,這樣就可以應(yīng)用連續(xù)的彈塑性力學(xué)對(duì)其進(jìn)行理論研究。此外,由于土體與生物質(zhì)粉末體的性質(zhì)有很大的相似性,即屈服過(guò)程伴隨有體積減小,土塑性力學(xué)認(rèn)為材料不僅可以產(chǎn)生軟化,而且可以屈服和硬化,并且與靜水壓力有關(guān),可以從土體塑性力學(xué)理論出發(fā),尋找建立生物質(zhì)秸稈致密變形過(guò)程的力學(xué)模。
非線性問題一般可用①增量法、②全量法(迭代法)和③混合法等方法進(jìn)行分析解決。
3.2.1增量法
增量法,它的基本思想是將載荷分解為有限個(gè)很小的載荷增量,每次一個(gè)增量。每步施加增量載荷后都將獲一個(gè)相應(yīng)的位移增量,把這些位移增量累加起來(lái)可以得最終位移。
分析非線性問題時(shí),先把載荷劃分為有限個(gè)載荷增量,計(jì)算過(guò)程中,每次施加一個(gè)載荷增量。實(shí)際上就是用一系列線性問題去近似非線性問題,把非線性曲線用分段線性的折線去代替。
3.2-2全量法
全量法又稱迭代法,這種求解方法也叫割線法。它是在每次迭代過(guò)程中都施加所有載荷,然后逐步調(diào)整位移和應(yīng)變,使?jié)M足非線性的應(yīng)力一應(yīng)變關(guān)系。一次施加所有載荷,然后逐步調(diào)整位移,使基本方程成立。
直接迭代法的思路為使用某個(gè)固定公式反復(fù)校正根的近似值,使其逐步精確,直到得出滿足精度要求的結(jié)果位置。首先給出一個(gè)近似的解,再由應(yīng)力一應(yīng)變關(guān)系逐步求出其相應(yīng)解,根據(jù)方程組可求得第一個(gè)改進(jìn)的近似解。然后重復(fù)計(jì)算,直至計(jì)算結(jié)果前后兩次充分接近為止。迭代計(jì)算如圖3-2所示。
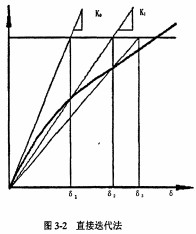
在直接迭代法中主要有牛頓一拉普森(Newton-Raphson)法,簡(jiǎn)稱NR方法,修正NR法,擬NR法等。
3.2.3混合法
混合法是同時(shí)利用了增量法和全量法。混合法的思想是把載荷劃分為有限級(jí)載荷增量,每級(jí)載荷增量的大小略有增加,在每一級(jí)載荷增量作用下,進(jìn)行迭代計(jì)算,使每一級(jí)載荷增量中的計(jì)算誤差控制在很小的范圍之內(nèi),從而得到比較精確的結(jié)果,如圖3-3所示。
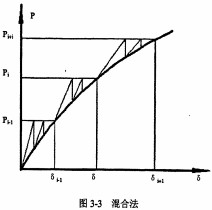
混合法集增量法和全量法的優(yōu)點(diǎn)于一身,在計(jì)算過(guò)程中減少了對(duì)每個(gè)載荷增量的計(jì)算;缺點(diǎn)是計(jì)算量仍然較大。相比之下,混合法的優(yōu)點(diǎn)更為突出,在分析有限元非線性問題時(shí),是應(yīng)用最為廣泛的一種方法。
ANSYS有限元中,通常是采用混合法解決問題。即采用增量法施加載荷,而對(duì)于每一個(gè)載荷步的計(jì)算采用全量法,本文采用混合法。
3.3彈塑性有限元法
生物質(zhì)粉末體與金屬粉末性質(zhì)有一定的相似之處,但是它們的力學(xué)特性卻也不近相同。在擠壓變形過(guò)程中,它的體積變形和密度增大是同時(shí)進(jìn)行的,但是粉末受擠壓摩擦的運(yùn)動(dòng)和變形情況卻不相同,而且均受粉末與粉末之間、模孔壁與粉末之間不均勻摩擦力的影響,粉末體內(nèi)部的運(yùn)動(dòng)和變形情況是不一致的,同時(shí),粉末的塑性變形也受到靜水壓力的影響。本文借鑒粉末塑性成型的方法來(lái)進(jìn)行研究。
在有限變形條件下,應(yīng)變一位移關(guān)系式是非線性的,平衡方程也是非線性的。通常用拉格朗日法和歐拉法兩種方法建立變形方程。拉格朗日法描述變形是采用變形前某一點(diǎn)的初始坐標(biāo);歐拉法描述變形是采用變形后某一點(diǎn)的坐標(biāo)。本文用歐拉法建立有限變形基本方程。
設(shè)A點(diǎn)變形前的坐標(biāo)為a,以變形后的坐標(biāo)x為自變量,則A點(diǎn)的移為:
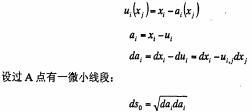


三門峽富通新能源主要生產(chǎn)和銷售
顆粒機(jī)、
秸稈壓塊機(jī)、飼料顆粒機(jī)、木屑顆粒機(jī)等生物質(zhì)燃料飼料等生物質(zhì)成型機(jī)械設(shè)備。同時(shí)我們還有大量的生物質(zhì)顆粒燃料出售。