����䷽�������I(y��)���a(ch��n)�е���Ҫ�h(hu��n)��(ji��)���䷽�ĺÉěQ�������a(ch��n)Ʒ���|(zh��)���ͽ�(j��ng)�I(y��ng)�ߵ����a(ch��n)Ч�棬��ˣ��䷽��ԭ�tͨ�����ڝM����B(y��ng)��(bi��o)��(zh��n)����r�±M�������䷽�ijɱ���Ҳ�����f��һ��(g��)��ͳɱ����@��һ��(g��)�dz���(f��)�s�y��Ć��}��һ��������ɷN�����M(j��n)����⣺����Ҏ(gu��)����Ŀ��(bi��o)Ҏ(gu��)�������У�����Ҏ(gu��)����Waugh��1951��������䑪(y��ng)����ԓ�I(l��ng)�����õ�����ձ飬������(d��o)˼���nj��䷽���}�þ���Ҏ(gu��)�����}��ģ�����Æμ��ͷ��M(j��n)����⣬���ھ���Ҏ(gu��)���Ą���̫��(qi��ng)����(d��o)������ԓ�����M(j��n)���䷽���r(sh��)���F(xi��n)�o�(y��u)�����rʮ���l�����o���ą�����Ҳ���m�ã���ˣ��@�N�����ڌ�(sh��)�H���a(ch��n)�аl(f��)�]��ָ��(d��o)���ò�����Ŀ��(bi��o)Ҏ(gu��)��������(y��ng)����ԓ�I(l��ng)���Ǟ��˿˷�����Ҏ(gu��)�����(y��u)������c(di��n)��Ŀ��(bi��o)Ҏ(gu��)����˼���������O(sh��)��һ��(g��)�ɽ��ܵijɱ�ֵ��Ȼ���ڃ�(y��u)�ȝM��ijЩ�����֣��s�������������s������r�«@�ýӽ�ԓ�ɱ�ֵ��һ��(g��)�䷽���@�N��������(du��)�ھ���Ҏ(gu��)�����Ը��`����@�õĽⲻ�ǿ����ã���Щ����ã���Щ�ⲻ���ã���?y��n)飬һ��(g��)���}�]���(y��u)�������ڼs���l���д��ڟo���M�����_ͻ�ļs����Ŀ��(bi��o)Ҏ(gu��)���ķ����Ǟ�ÿ��(g��)�s���x��һ��(g��)��(y��u)�ȼ�(j��)����(y��u)�ȼ�(j��)�ߵļs���ȝM�㣬��(d��ng)�Ñ���o���M�����_ͻ�ļs���x�ϸ߃�(y��u)�ȼ�(j��)�r(sh��)����(hu��)��(d��o)��ϵ�y(t��ng)�Ľⲻ���ã��෴���ã��C�ϣ�����Ҏ(gu��)����Ŀ��(bi��o)Ҏ(gu��)�����Dz��Ô�(sh��)�W(xu��)������(du��)�䷽���}�M(j��n)����⣬��Y(ji��)�������ڲ��M����ĵط������磬����Ҏ(gu��)������(sh��)��r�����(y��u)�⣬Ŀ��(bi��o)Ҏ(gu��)����ī@�������˞����ijЩ�s������r(ji��)����ˣ��҂��б�Ҫᘌ�(du��)����䷽���}̽��һ��(g��)�����Ќ�(sh��)�Hָ��(d��o)���x�Ć��}��ⷽ���������P(gu��n)�Y���У�Bruin����������ö�Agentϵ�y(t��ng)���һ�N���⾀��Ҏ(gu��)�����}����Փģ�ͣ�ԓģ��������YԴ���䣬������(g��)Agent����m��(g��)�YԴ��ÿ��(g��)Agent���Լ����΄�(w��)���ஔ(d��ng)�ڼs���M�㆖�}�������O(sh��)��Agent��������r��(g��)�YԴ�r(sh��)��ԓagent����(du��)��(y��ng)�Ć��}�н⣬ԓģ�ͽ�Q���䂀(g��)Agentͨ�^�f(xi��)�̷�ʽ�f(xi��)�{(di��o)�YԴ�����Ć��}�����õķ������ڱ����YԴ����(sh��)��׃��ǰ���£�AgentA�p��һ���ı���ռ��agent B����(y��ng)����һ���ı���ռ���ɂ�(g��)Agent���ԅf(xi��)��ܵ��ȡֵ�����ľ����ڽ��b���īI(xi��n)[2]��˼������˴�����(sh��)�(y��n)�о��Ļ��A(ch��)�������һ��(g��)���ڶ�Agentϵ�y(t��ng)���䷽���}���ģ�͡�
���T�{��ͨ����Դ���a(ch��n)�����
�w���C(j��)���w���C(j��)����ϙC(j��)�M���B(y��ng)ֳ���e(cu��)���x��
1������䷽���}��(ji��n)��
����䷽���}��(ji��n)��֮���nj����N���ԭ����һ�����������һ��õ�һ�N��Ϻ����ϣ�Ҫ��ԓ����е�ijЩ�I(y��ng)�B(y��ng)�ɷ��_(d��)����ij�N��(d��ng)��ģ���B(y��ng)��(bi��o)��(zh��n)��
��4��1�(y��u)��s���M����r��
��1�����x���1��ʾ“���L(zh��ng)�i0��120kg��ʳ3075g NRC_98”����B(y��ng)��(bi��o)��(zh��n)��ԭ���x����r���2��ʾ���õ��D1��ʾ�Ĕ�(sh��)�W(xu��)ģ�ͣ����ڝM��s���l��(1)��(11)��ǰ���£���Ŀ��(bi��o)����(sh��)z����Сֵ����ͳɱ��������þ���Ҏ(gu��)��������(du��)ԓ���}��⣬�ɵõ����3��ʾ���(y��u)�⣬�s���M����r���4��ʾ��

��1 ��Ϙ�(bi��o)��(zh��n)��Ҫ��ĸ��I(y��ng)�B(y��ng)Ԫ�غ���
|
����ָ��(bi��o) |
��(bi��o)��(zh��n)ֵ��%�� |
|
������ |
3.40 |
|
�ֵ��� |
13.20 |
|
�} |
0.45 |
|
�� |
0.40 |
|
ه���� |
0.60 |
|
������ |
0.23 |
��2�Nԭ�ϼ��I(y��ng)�B(y��ng)�ɷֺ�������λ��Ԫ����/ǧ�ˣ�%��
|
׃�� |
ԭ���� |
�r(ji��)��Ԫ�� |
�������� |
�������� |
������ |
�ֵ��� |
�} |
�� |
ه���� |
������ |
|
X1 |
���� |
0.9 |
45 |
99.9 |
3.41 |
8.7 |
0.02 |
0.27 |
0.24 |
0.18 |
|
X2 |
���� |
1.27 |
0 |
99.9 |
2.24 |
15.7 |
0.11 |
0.92 |
0.58 |
0.13 |
|
X3 |
���� |
2.86 |
0 |
99.9 |
3.25 |
43 |
0.32 |
0.61 |
2.45 |
0.64 |
|
X4 |
������ |
1.48 |
3 |
5 |
2.26 |
42.5 |
0.24 |
0.97 |
1.59 |
0.45 |
|
X5 |
���� |
8 |
0 |
99.9 |
7.7 |
|
|
|
|
|
|
X6 |
ʯ�� |
0.2 |
0 |
99.9 |
|
|
35.85 |
|
|
|
|
X7 |
������} |
2 |
0 |
99.9 |
|
|
23.20 |
18 |
|
|
|
X8 |
������ |
36 |
0 |
0.7 |
|
|
|
|
|
98 |
|
X9 |
ه���� |
28 |
0 |
99.9 |
|
|
|
|
78 |
|

��һ�(y��)

��ԭ�t���õ����C���Y(ji��)Փ���C�� �C����
����1�����ij�䷽���}�����(y��u)�⣬�t���㷨һ�����ҵ�ԓ�(y��u)�⣮
�C�������㷨֪���㷨�Y(ji��)���ڃɷN��r��һ�N������Agent��̎��satisfied��B(t��i)����һ�N�Dz����ھ���unsatisfied��B(t��i)��Agent��������㷨�Y(ji��)���ڵ�1�N��r��������1���㷨�õ��Ľ����(y��u)�⣬����㷨�Y(ji��)���ڵ�2�N��r���t�㷨�õ���һ�������(y��u)�⣬�F(xi��n)���C���㷨����(hu��)�Y(ji��)���ڵ�2�N��r�����O(sh��)�㷨�Y(ji��)���ڵ�2�N��r�����õ�����= Xl��X2��…��i�����˕r(sh��)�㷨�чLԇ�����п��ܵķ���������ʧ�����@�c���}�����(y��u)��ì�ܣ��Y(ji��)Փ���C�� �C����
6��(sh��)�(y��n)�Y(ji��)��������
6.1���(y��u)�����r
��(du��)�����(y��u)��Ć��}������1��������(sh��)�(y��n)�Y(ji��)����D2���D3���D4��ʾ�����У�z�S��ʾ�f(xi��)��݆��(sh��)���D2��ʾ�f(xi��)���^���Ї��ɱ���ȡֵ׃����r���D3��ʾ�f(xi��)���^���и�ԭ����ȵ�ȡֵ׃����r���D4��ʾ�s���l���Č�(sh��)�Hֵһ��(bi��o)��(zh��n)ֵ�S�f(xi��)���^�̵�׃����r��
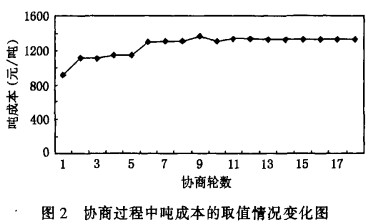
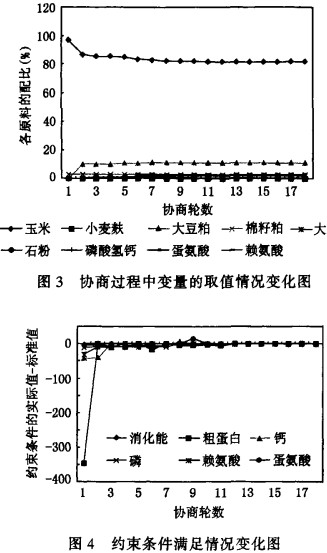
�������ĈD�п��Կ������㷨��K�Ք���һ��(g��)�(y��u)�⡣
6.2�]���(y��u)�����r
��(du��)�ڛ]���(y��u)��Ć��}���o����5��ʾ�Nԭ�ϼ���I(y��ng)�B(y��ng)�ɷֺ������քe�þ���Ҏ(gu��)����Ŀ��(bi��o)Ҏ(gu��)���Ͷ�Agentϵ�y(t��ng)����⣬�s���M����r���6��ʾ����D���ʾ��D5��ʾ�����У�z�S��ʾ���Ǽs���l��������8��(g��)�s����y�S��ʾ�s���l�����㷨�Y(ji��)���r(sh��)��ȡֵ��r����(sh��)�HֵһĿ��(bi��o)ֵ����
��5�N����䷽ԭ�ϼ���I(y��ng)�B(y��ng)�ɷֺ�������λ��Ԫ����/ǧ�ˡ�%��
|
׃�� |
ԭ���� |
�r(ji��)�� |
�������� |
�������� |
������ |
�ֵ��� |
�} |
�� |
ه���� |
������ |
��+�� |
ɫ���� |
|
X1 |
���� |
0.9 |
45 |
99.9 |
3.41 |
8.7 |
0.02 |
0.27 |
0.24 |
0.18 |
0.38 |
0.07 |
|
X2 |
�� |
2.4 |
0 |
10 |
3.97 |
35.50 |
0.27 |
0.48 |
2.00 |
0.48 |
1.03 |
0.56 |
|
X3 |
��� |
2.19 |
0 |
99.9 |
3.23 |
40.90 |
0.30 |
0.49 |
2.38 |
0.59 |
1.20 |
0.63 |
|
X4 |
ʯ�� |
0.2 |
0 |
99.9 |
|
|
35.85 |
|
|
|
|
|
|
X5 |
������} |
2 |
0 |
99.9 |
|
|
23.20 |
18 |
|
|
|
|
|
X6 |
4%�A(y��)���� |
3 |
4 |
4 |
|
|
18.00 |
15.00 |
3.00 |
2.00 |
|
|
��6�քe�þ���Ҏ(gu��)����Ŀ��(bi��o)Ҏ(gu��)���Ͷ�Agentϵ�y(t��ng)�����õ��ijɱ����s���M����r������λ��%��Ԫ/����
|
���}��ⷨ |
��(sh��)�Hֵ-��(bi��o)��(zh��n)ֵ��%�� |
|
������ |
�ֵ��� |
�} |
�� |
ه���� |
������ |
ɫ���� |
��+�� |
�ɱ� |
|
����Ҏ(gu��)������ֵ�� |
0.01 |
6.99 |
-0.15 |
5.79 |
0 |
9.39 |
0.69 |
14.04 |
1149.21 |
|
��Agent����ֵ�� |
0.066 |
0.002 |
0.205 |
0.297 |
-3.977 |
7.297 |
0.038 |
13.963 |
1122.206 |
|
Ŀ��(bi��o)Ҏ(gu��)������ֵ�� |
-0.213 |
64.194 |
-0.004 |
-9.512 |
0 |
8.155 |
-0.4 |
15.666 |
1134.2 |
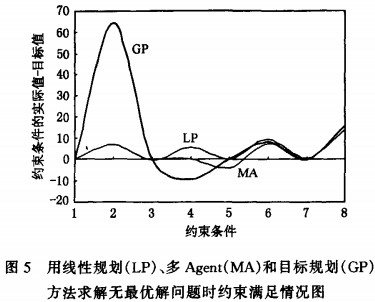
�������ĈD���҂����Կ������ö�Agent������õĽ�ʹ���}�и��s���M�����ã�������ƽ��������?y��n)飬����䷽���}��(qi��ng)�{(di��o)�I(y��ng)�B(y��ng)�ɷֵı�����ֻ�РI(y��ng)�B(y��ng)�ɷ֝M��һ�������r(sh��)����(d��ng)�(du��)�I(y��ng)�B(y��ng)���յ����.���@��(g��)���}�У�����Ҏ(gu��)���ڰl(f��)�F(xi��n)���}�o�(y��u)��r(sh��)�Y(ji��)�����Y(ji��)���r(sh��)��׃���Į�(d��ng)ǰֵ���㷨�Ľ⣻Ŀ��(bi��o)Ҏ(gu��)�������O(sh��)��һ��(g��)���ɱ�1130.00��Ȼ���ٌ����s�����σ�(y��u)�ȼ�(j��)����(y��u)�ȼ�(j��)�ߵļs����(y��u)�ȝM�㣬�����Ѓ�(y��u)�ȿ��]25��ه���ᣩ��23���}������������6��ʾ����Agent���������Д��26�������ᣩ��z8����+�ף��鲻�ɝM��(unsatisfiable)�s�������ԣ��^���Д���s��z5�cZ��Z2��Zl3��Zl4��Zl7���_ͻ��ͬ�Ӻ���……��K�õ��P(gu��n)��Z2��27���(y��u)�⣬������(g��)���}�Ľ��ƽ⣬�@Ȼ���@��(g��)�⃞(y��u)�ھ���Ҏ(gu��)����Ŀ��(bi��o)Ҏ(gu��)���Ľ⣮
7�Y(ji��) Փ
���������һ�N���ڶ�Agentϵ�y(t��ng)������䷽��(y��u)���㷨����(du��)�����(y��u)��Ć��}��ԓ�㷨�܉�ƽ��(y��u)�⣬��(du��)�ڛ]���(y��u)��Ć��}��ԓ�㷨�o���Ľ��ƽ⃞(y��u)��Ŀ��(bi��o)Ҏ(gu��)�������õ��Ľ⡣ͨ�^��(sh��)�H��(y��ng)�ã��ѽ�(j��ng)�C����ԓ�����ó��Ľ�����Ќ�(sh��)�H��(y��ng)�Ãr(ji��)ֵ�����⣬ԓ�㷨߀����һ���ĿɔU(ku��)չ�ԣ������ԔU(ku��)չ����һ��ľ���Ҏ(gu��)�����}���������ĈD���҂����Կ������ö�Agent������õĽ�ʹ���}�и��s���M�����ã�������ƽ��������?y��n)飬����䷽���}��(qi��ng)�{(di��o)�I(y��ng)�B(y��ng)�ɷֵı�����ֻ�РI(y��ng)�B(y��ng)�ɷ֝M��һ�������r(sh��)����(d��ng)�(du��)�I(y��ng)�B(y��ng)���յ���ã����@��(g��)���}�У�����Ҏ(gu��)���ڰl(f��)�F(xi��n)���}�o�(y��u)��r(sh��)�Y(ji��)�����Y(ji��)���r(sh��)��׃���Į�(d��ng)ǰֵ���㷨�Ľ⣻Ŀ��(bi��o)Ҏ(gu��)�������O(sh��)��һ��(g��)���ɱ�1130.00��Ȼ���ٌ����s�����σ�(y��u)�ȼ�(j��)����(y��u)�ȼ�(j��)�ߵļs����(y��u)�ȝM�㣬�����Ѓ�(y��u)�ȿ��]25��ه���ᣩ��23���}������������6��ʾ����Agent���������Д��26�������ᣩ��z8����+�ף��鲻�ɝM��(unsatisfiable)�s�������ԣ��^���Д���s��z5�c21��22��23��24��27���_ͻ��ͬ�Ӻ���……��K�õ��P(gu��n)��zz��27���(y��u)�⣬������(g��)���}�Ľ��ƽ⣬�@Ȼ���@��(g��)�⃞(y��u)�ھ���Ҏ(gu��)����Ŀ��(bi��o)Ҏ(gu��)���Ľ⡣
7�Y(ji��) Փ
���������һ�N���ڶ�Agentϵ�y(t��ng)������䷽��(y��u)���㷨����(du��)�����(y��u)��Ć��}��ԓ�㷨�܉�ƽ��(y��u)�⣬��(du��)�ڛ]���(y��u)��Ć��}��ԓ�㷨�o���Ľ��ƽ⃞(y��u)��Ŀ��(bi��o)Ҏ(gu��)�������õ��Ľ⡣ͨ�^��(sh��)�H��(y��ng)�ã��ѽ�(j��ng)�C����ԓ�����ó��Ľ�����Ќ�(sh��)�H��(y��ng)�Ãr(ji��)ֵ�����⣬ԓ�㷨߀����һ���ĿɔU(ku��)չ�ԣ������ԔU(ku��)չ����һ��ľ���Ҏ(gu��)�����}��
���T�{��ͨ����Դ���a(ch��n)������w���C(j��)���w���C(j��)��
�ն����K�C(j��)��
ľм�w���C(j��)���B(y��ng)ֳ�������a(ch��n)����ȼ�ϼӹ��S���e(cu��)���x��


 ��һ�(y��)
��һ�(y��)


